Amortized Fee Setup
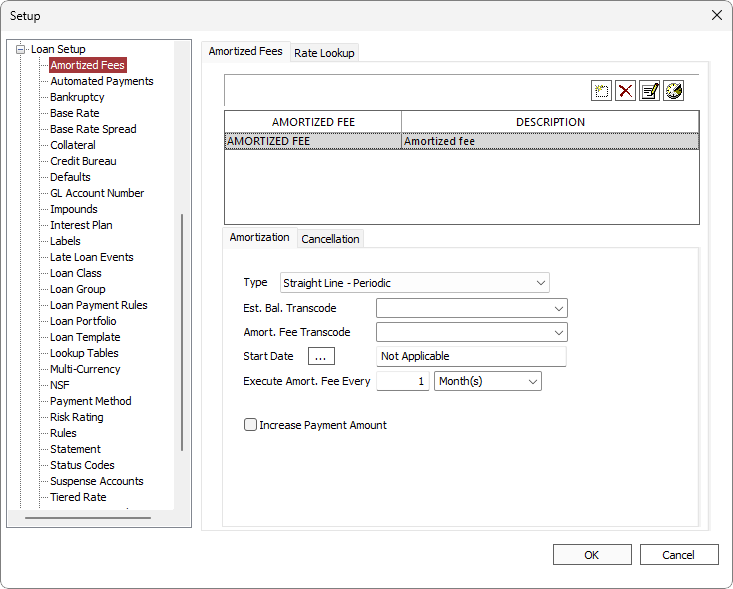
Some of the parameters for amortized fees can be pre-defined and saved as templates in Setup > Loan Setup > Amortized Fees. The templates can then be selected when setting up an amortized fee on a loan and the configured parameters will be filled in accordingly. The description of the fields can be found in their respective amortization type sections below.
Click  next to Start Date to configure the start date that will be filled in for the amortized fee when the template is selected.
next to Start Date to configure the start date that will be filled in for the amortized fee when the template is selected.
| Type | Defines the method by which the date is determined.
|
||||
| Day Value | Forces the date to a specific day of the month.
|
||||
| Date | This field is not applicable and is disabled. |
Configuring Amortized Fee on a Loan
To set up an amortized fee on a loan, query the loan, then click the Loan tab of the ribbon bar and select  Amortized Fees in the Setup group.
Amortized Fees in the Setup group.
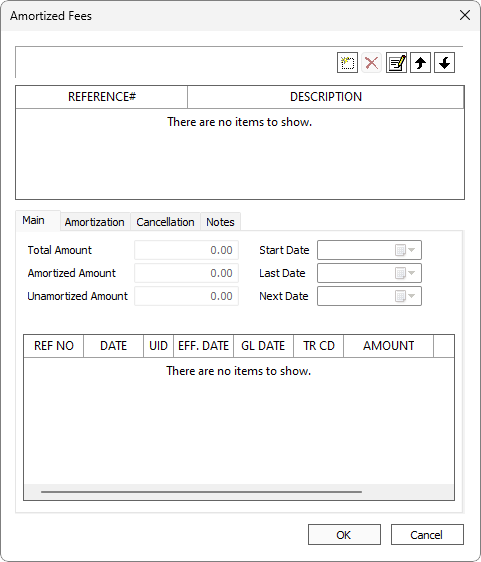
Click Add .
.
Select <MANUAL> from the Template drop down list to start with a clean slate or select a pre-defined template to work with. The specific configuration will depend on the type of fee amortization:
If a fee is amortized via the straight line method, the amount of the fee to be amortized is divided by the total number of periods, and the periodic amortization transaction will be run for the resulting amount whenever called for by the fee amortization setup.
Examples
- A $1,000 fee, amortized monthly over 12 months: The amortization transaction will occur once a month for the amount of $83.33.
- A $1,000 fee, amortized daily over 12 months: The amortization transaction will occur daily for the amount of $2.74.
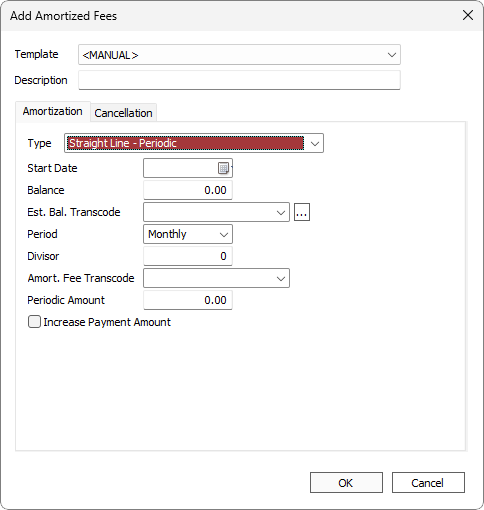
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Set to Straight Line - Periodic. |
| Start Date | The first date on which the fee should amortize |
| Balance | The Amount of the fee to Amortize |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. Note that Effective Date is not applicable to this amortization type. to configure additional parameters. Note that Effective Date is not applicable to this amortization type. |
| Period | The frequency of the straight line amortization |
| Divisor | The total number of times that the fee will amortize straight line. The fee amount will be divided by this value to derive the periodic amount. |
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Periodic Amount | The amount that will be amortized during each periodic amortization. |
| This option is to be used when an amortized fee, such as an insurance premium, requires a separate billing (effectively increasing the payment amount). When selected, two separate billings will be generated; one for principal + interest and another for premium + interest. The establishing transaction code (e.g. Transaction Code 190) must be configured to increase the principal. |
The custom method of fee amortization is the simplest (and also the least used) method by which to amortize a fee.
You simply specify the exact dates on which portions of the fee are scheduled to be amortized then you specify the exact amount to be amortized on each of those dates.
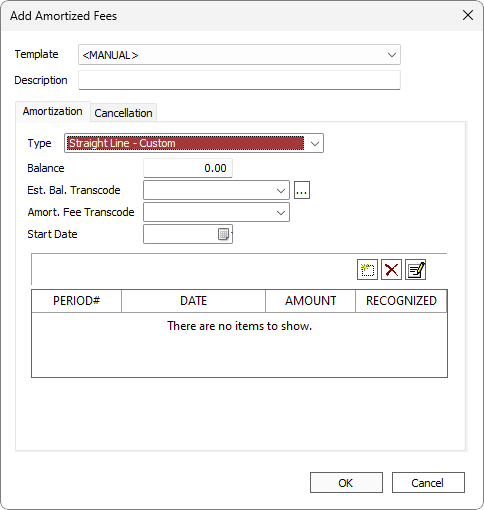
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Select Straight Line - Custom. |
| Balance | The Amount of the fee to Amortize |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. Note that Effective Date is not applicable to this amortization type. to configure additional parameters. Note that Effective Date is not applicable to this amortization type.
|
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Start Date | The date of the first amortization and calculation. |
To schedule a date and amount to amortize a portion of the fee, click Add on the lower section of the dialog.
on the lower section of the dialog.
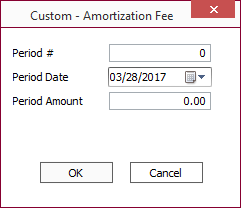
| Period Number | Enter an identifying number for the period that you are defining. |
| Period Date | Enter a date on which you want a portion of the fee to be amortized. |
| Period Amount | Enter the amount that represents the portion of the fee that you want amortized. |
NLS 5.42 and before
Known as Effective Interest Method prior to NLS 5.43.Effective Interest Method - On Payment is used to obtain the amortized amount based on the given parameters from actual interest paid when payments are made on the due date.
The equation for this amortization method is:
Amortized Amount = Actual Interest Paid – Interest Calculated from Amortized Schedule
Where Interest Calculated from Amortized Schedule is the amortization schedule of the Principal Amount (Loan Principal Bal + Starting Balance) and Effective Interest Rate.
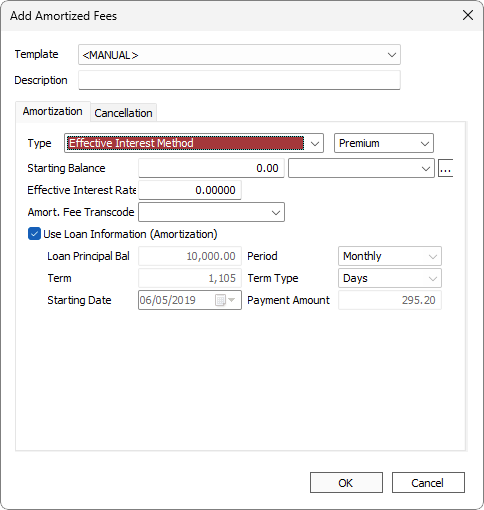
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Select Effective Interest Method. Premium/Discount setting is only for classification purposes and does not affect the calculation. |
| Starting Balance | The amount of the fee to amortize. |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. Note that Effective Date is not applicable to this amortization type. to configure additional parameters. Note that Effective Date is not applicable to this amortization type. |
| Effective Interest Rate | The interest rate. |
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Use Loan Information | Deselect and enter the desired values to amortize on values different from the loan. |
Effective Interest Method - Scheduled is used to obtain the amortized amount based on the given parameters from actual interest paid based on the effective interest rate as calculated by the internal rate of return (IRR) calculation. Often used where finance charges are used in lieu of an interest on the loan.
For fixed amortization loans use ACT/ACT interest year, end of day accrual, and amortize based on actual interest year amortization method.
The equation for this amortization method is:
Payment = Loan Principal Balance + Starting Balance
Where Interest Calculated from Amortized Schedule is the amortization schedule of the Principal Amount (Loan Principal Bal + Starting Balance) and Effective Interest Rate.
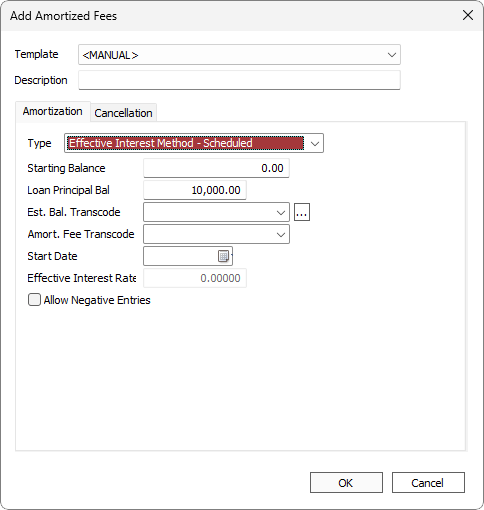
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Select Effective Interest Method - Scheduled |
| Starting Balance | The amount of the fee to amortize. |
| Loan Principal Bal | Principal balance of the loan. |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. Note that Effective Date is not applicable to this amortization type. to configure additional parameters. Note that Effective Date is not applicable to this amortization type. |
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Effective Interest Rate | The interest rate as calculated by the IRR calculation based on the initial principal. |
| Allow Negative Entries | If selected and the amount of the fee to amortize comes to a negative value, then that amount will be rolled back (un-amortized). If not selected and the amount of the fee to amortize comes to a negative value, then zero will be amortized. |
Example - No Interest Loan
Principal balance of the loan is 1,480,000.The finance charge on this loan takes the form of a fee in the amount of 120,000.
The full loan amount is to be repaid over 12 months.
1,480,000 + 120,000 = 1,600,000
1,600,000 / 12 = 133,333.33 (monthly payment)
The loan is entered as a 1,600,000 principal only loan with 12 payments of 133,333.33.
The final payment will be 133,333.37.
The amortized fee is set up using the effective interest method.
The Effective Interest Rate is based on the IRR calculation.
12 monthly payments of 133,333.33 based on an initial principal value of 1,480,000 yields an effective interest rate of: 14.61672%. Utilizing an amortization schedule based on a loan of 1,480,000 @14.61672% over 12 months, the schedule for the amortization of the fee will be calculated. The remaining 2 cents for rounding will be amortized in the final period.
Note that this amortization schedule is NOT the amortization schedule of the loan, which is a principal only loan. It is used simply for calculating the schedule for amortizing the fee.
Example - Interest Bearing Loan
Principal balance of the loan is 1,480,000.The finance charge on this loan takes the form of a fee in the amount of 120,000.
The full loan amount is to be repaid over 12 months.
Loan has an interest rate of 10% using ACT/ACT interest year.
Monthly payment amount on 1,600,000 is 140,678.71.
The setup for the amortized fee of 120,000 is identical to the previous example. The effective interest rate is that rate which would result in the same payment of 140,678.71 if the principal were 1,480,000 (1,600,000 – 120,000). This is calculated using the IRR calculation as 24.97053%.
To create the schedule of the fee amortization, the interest portion of the amortization schedule between 1,600,000 @10% and 1,480,000 @24.97053% are compared.
The difference between the calculated interest portions of the payments in any one month will be the fee amortization for that month.
Payment #1: 31,301.85 – 13,551.91 = 17,749.94.
The calculation for all subsequent months is identical.
The sum of all interest payments: 208,144.55 – 88,144.53 = 120,000.02
The remaining 0.02 is the rounding error within the expected threshold and is amortized in the final month.
If a fee is amortized via the Effective Interest Method - Daily Accrual, the amortization of the fee will track with the interest accruals on the loan. For example: in an amortized loan, more interest tends to be realized up front while the principal balance is higher. A fee amortized by the effective interest method would amortize in proportion to this accrual of interest.
The equations and procedures for this amortization method are as follows:
Given that
x = total interest accrued life to date on the loan
y = total interest projected to accrue over the entire life of the loan based on history so far and projecting the payment schedule forward from this point to the maturity date
then
x/y = the ratio of the fee which should be amortized up to this point in time.
if
f = the amount of the fee to be amortized
then
f* (x/y) = the dollar amount of the fee that should be amortized up to this point in time.
if
a = the amount of the fee that has been amortized so far
then
(f * (x/y)) -a = the amount of the fee to amortize today.
The amortization period controls the frequency with which these calculations are run. Modifications, interest rate changes, advances, or principal reductions on a loan can cause drastic shifts to the factor “y” in the equations above and as a result when these calculations are run, the amount of the fee to amortize can jump greatly, or can even be a negative value. There is a checkbox to allow negative amortization, and if this is selected, the fee amortization will correct back to where it “should be” given the new and current conditions of the loan. If this checkbox is not selected, then the amount amortized will be zero each time until such time as the calculations yield a positive amount to amortize. Because the projection of interest “y” is always through the maturity date of the loan, by that date y will always equal x, and consequently the fee will always amortize in full on the first amortization date on or after the date of maturity.
NLS 5.33 and later
For effective interest method - daily accrual, a mathematical amortization method is used under certain conditions to improve the speed of accruals. The traditional method is used when one of the following conditions is true:- Compounding of interest exist
- Using base rate
- Using tiered rate
- Using introductory rate
- Using step days in main section
- Using step amount in main section
- Using stream 2 and the destination is current_interest_balance
Any difference between the mathematical and actual amortization methods can be viewed in the trace file under AMORTIZATION SCHEDULE ANTICIPATED INTEREST.
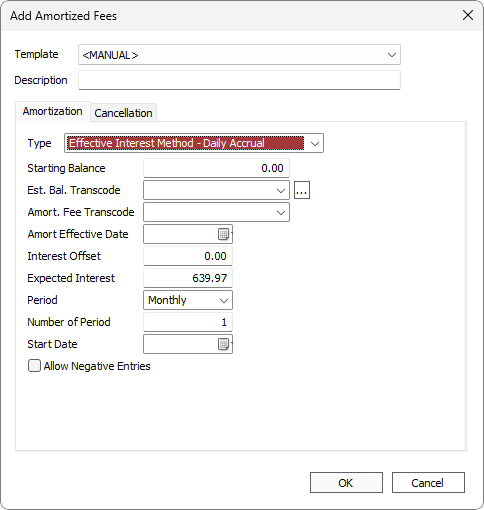
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Select Effective Interest Method - Daily Accrual. |
| Starting Balance | The Amount of the fee to Amortize |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. to configure additional parameters. |
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Amort Effective Date | The date from which to start amortizing. Interest accrued prior to this date is not counted in either “x” or “y.” |
| Interest Offset | This field is calculated automatically, and is the amount to be deducted from “x” and “y” based on the Amort Effective Date. It represents the interest that accrued prior to that date. |
| Expected Interest | Factor “y” in the above equations |
| Period | The period used to define the frequency of the amortization |
| Number of Periods | Used with period to define the frequency of the amortization. Example If period is set to days and number of periods is set to 5, the calculations above would be run every five days. |
| Start Date | The date of the first amortization and calculation. |
| Allow Negative Entries | If selected and the amount of the fee to amortize comes to a negative value, then that amount will be rolled back (un-amortized). If not selected and the amount of the fee to amortize comes to a negative value, then zero will be amortized. |
If a fee is amortized via the principal/original balance pro-rata method, the amortization of the fee will track with the rate at which the principal balance on the loan is repaid. For example, when 20% of the original principal of the loan has been repaid, the fee will be 20% amortized.
The equations and procedures for this amortization method are as follows:
Given that
x = the total principal paid on the loan
y = the total principal advanced on the loan
then
x/y = the ratio of the fee which should be amortized up to this point in time.
if
f = the amount of the fee to be amortized
then
f * (x/y) = the dollar amount of the fee that should be amortized up to this point in time.
if
a = the amount of the fee that has been amortized so far
then
(f * (x/y)) - a = the amount of the fee to amortize today.
As long as no principal payments have been made since the last time the calculations were run, the amount of the fee to amortize will always come out to zero. Therefore, if it is your intention that a portion of the fee should amortize as soon as a principal payment is made, set the period for this setup to daily. A portion of the fee will always amortize during the nightly accrual process of any day on which there was a payment to principal.
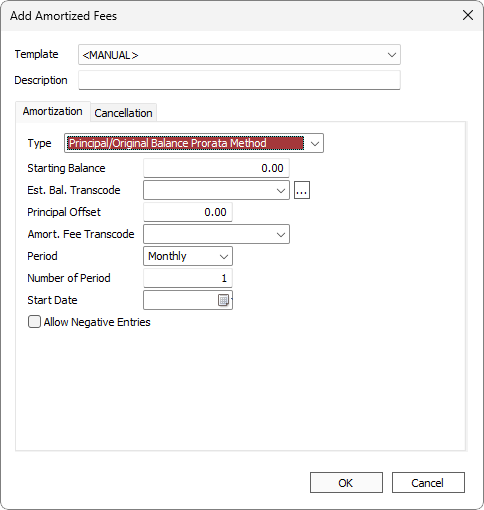
| Description | Descriptive text to identify this amortized fees and distinguish it from any other amortized fees on the same loan. |
| Type | Select Principal/Original Balance Prorata Method. |
| Starting Balance | The Amount of the fee to Amortize |
| Est. Bal. Transcode | The Establishing Transaction Code. Only transaction codes which meet the requirements for an Amortized Fee establishing transaction code will be available in this drop down list.
Click  to configure additional parameters. Note that Effective Date is not applicable to this amortization type. to configure additional parameters. Note that Effective Date is not applicable to this amortization type. |
| Principal Offset | The amount to be deducted from the principal paid “x” and principal advanced “y” of the loan. Amortization beginning on the start date will be based on this adjusted principal. |
| Amort. Fee Transcode | The periodic amortizing transaction code. Only transaction codes which meet the requirements for an Amortized Fee periodic amortizing transaction code will be available in this drop down list. |
| Period | The period used to define the frequency of the amortization |
| Number of Periods | Used with period to define the frequency of the amortization. Example If period is set to days and number of periods is set to 5, the calculations above would be run every five days. |
| Start Date | The date of the first amortization and calculation. |
| Allow Negative Entries | If selected and the amount of the fee to amortize comes to a negative value, then that amount will be rolled back (un-amortized). If not selected and the amount of the fee to amortize comes to a negative value, then zero will be amortized. |
If the loan’s Interest Type is set to Fixed Amortization, the principal paid for the above calculations is the amount of principal that should have been paid according to the amortization schedule. This means that the fee will amortize on the next opportunity to do so after a principal payment is due, even if that principal payment has not been made.
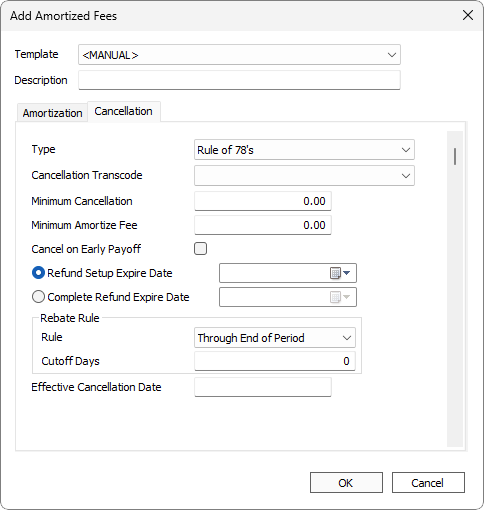
This method will amortized the fee following the rule of 78.
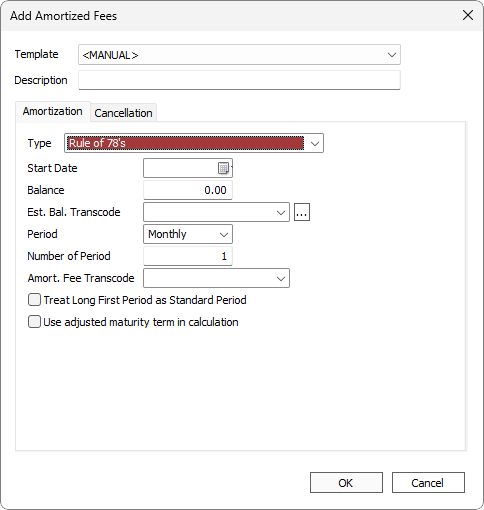
If the term type is daily, the pro-rata share of the periodic rule of 78 amortization for that month is amortized.
Example
$100 fee on a 12/12 loan will be (12/78) * 100 = $15.38461. Then $15.38461/31 Days in Month = $0.496277.This method will amortize using the rule of 78 then do a secondary amortization using the straight line method and take the average of the two amortizations.
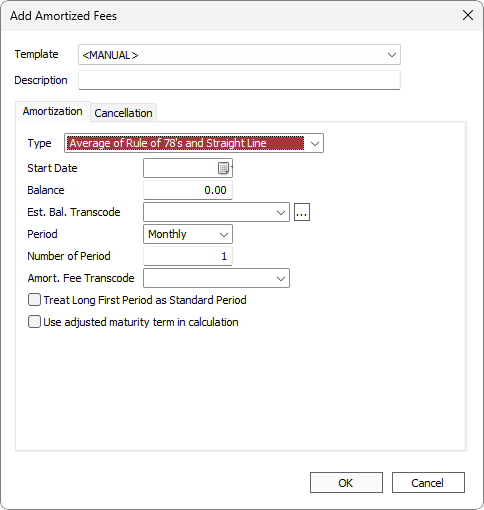
Example
Using rule of 78, $100 fee on a 12/12 loan will be (12/78) * 100 = $15.38461.Using straight line, $100/12 = $8.33333, so the average of rule of 78 and straight line will be (15.38461 + 8.33333)/2 = $11.858971 for the first month if there are 31 days in the month.
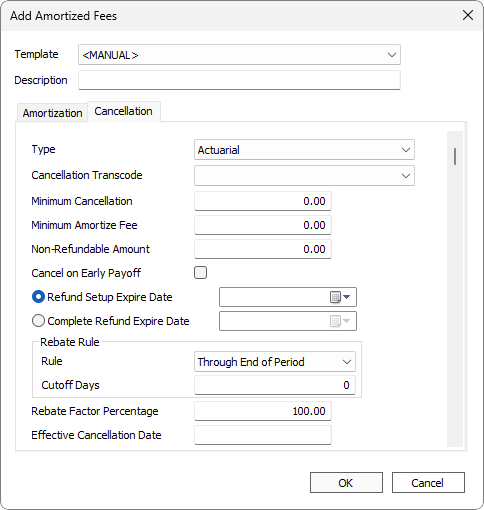
This will amortize using the actuarial method.
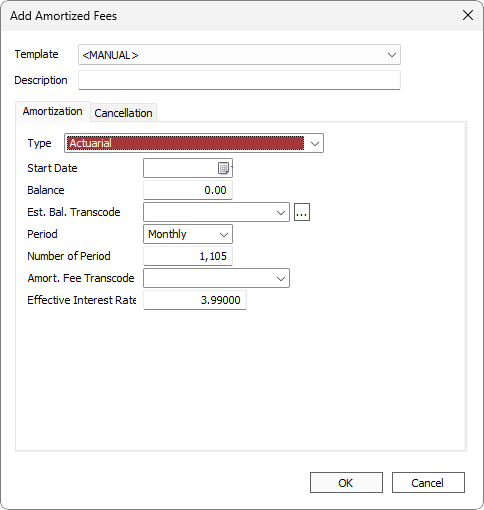
The equation for this amortization method is:
I = Interest rate / 12
N = Number of months in loan term
M = Number of months in insurance term
T = Number of months elapsed from amortization start date to refund date
Present Value Formula at N months = (1 - (1 / (1 + I)) ^ N) / I
Present Value Formula at (N - T) months = (1 - (1 / (1 + I)) ^ (N - T)) / I
Present Value Formula at (N - M) months = (1 - (1 / (1 + I)) ^ (N - M)) / I
Unearned Premium = Original Premium * (Remaining Term - Present Value Formula at (N - T) months - Present Value Formula at (N - M) months) / (Insurance Term - Present Value Formula at N months - Present Value Formula at (N - M) months)
Earned Premium = Original Premium - Unearned Premium
Example
The original premium is 200.00.
The remaining term is 57 months.
The elapsed term is three months.
The interest rate is 25%.
The loan term is 60 months.
The insurance term is 60 months.
I = .020833
N = 60
M = 60
T = 3
Present Value Formula at N months = (1 - (1 / (1 + .020833)) ^ 60) / .020833 = 34.0702863
Present Value Formula at (N - T) months = (1 - (1 / (1 + .020833)) ^ 57) / .020833 = 33.1813811
Present Value Formula at (N - M) months = (1 - (1 / (1 + .020833)) ^ 0) / .020833 = 0
Unearned Premium = 200.00 * (57 - 33.1813811 - 0) / (60 - 34.0702863 - 0) = 183.716791 = 183.72
Earned Premium = 200.00 - 183.72 = 16.28
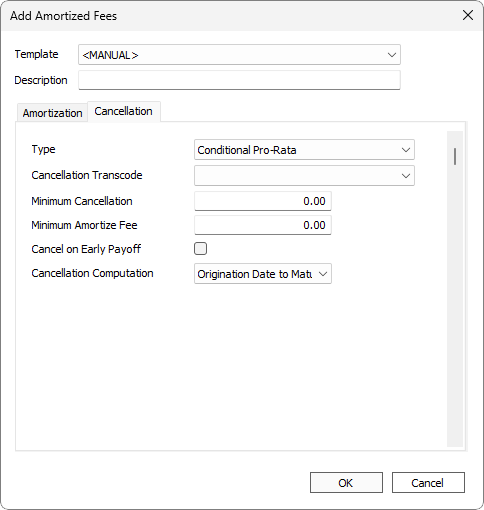
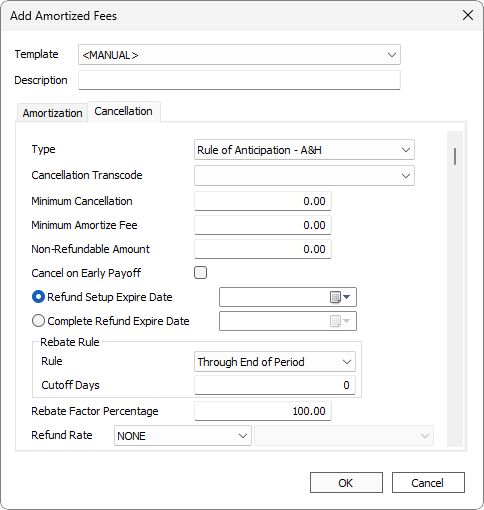
| Type |
Calculation used to determine the amortization adjustment and cancellation amounts.
|
|||||
| Cancellation Transcode | Transaction code to use with the cancellation. | |||||
| Minimum Cancellation | Sets the minimum amount required for the cancellation amount. Cancellation amount is 0 if it is less than the minimum cancellation value. Maximum value is 999.00. | |||||
| The minimum amount that may be assessed on the loan.
Example If the closing fee of a loan is $30 and the loan is paid off before maturity, setting this to $25 will still asses $25 fee on the loan. |
||||||
| The amount that is to be excluded from the total amortized fee amount prior to calculating the refund amount. | ||||||
| Cancel on Early Payoff | When selected, the entire amortized fee is removed when the loan is paid off early. | |||||
| No refund of amortized fees is issued on or after the specified date. Example If the closing fee can only be refunded within the first 90 days and the lender is allowed to keep the full amount after 90 days, advance this date 90 days from the origination date. |
||||||
|
Complete Refund Expire Date5.20+
|
A full refund of amortized fees is issued on or before the specified date. | |||||
| Rebate Rule | Rules for rebate determination.
|
|||||
| Only applicable to type Pro-Rata. The percentage of the refund amount (unamortized fee) portion to be included in the total cancellation amount. | ||||||
|
Cancellation Computation5.16+
|
Only applicable to type Conditional Pro-Rata.
|
|||||
|
Refund Rate5.38+
|
Only applicable to Rule of Anticipation. Select from refund rate(s) as configured in Setup > Loan Setup > Amortized Fees > Rate Lookup. When a selection is made, the most recent rate will be shown to the right of this field. |
Rate Lookup
NLS 5.38 and later
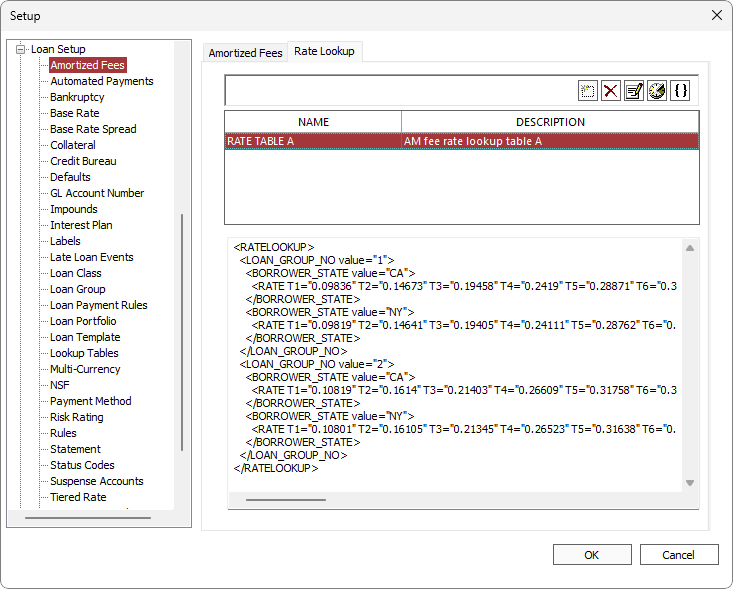
Rate lookup is used by the “Rule of Anticipation - A&H” cancellation type. A rule is defined as an XML using <RATELOOKUP> as the root element and <RATE> as a leaf node.
The XML is parsed from top to bottom and the rate specified for the first matching criteria will be used.
To specify a default rate for when there is no match, specify a <RATE> element under <RATELOOKUP> at the end of the XML. Specifying a <RATE> element at the top of the XML will result in that rate always being used regardless of any matching criteria below it.
Click  to check the validity of the XML.
to check the validity of the XML.
<RATELOOKUP>
| Attribute | Comments |
|---|---|
| No attribute | Root element. |
<LOAN_GROUP_NO>
| Attribute | Comments |
|---|---|
| Value | The loan group number. Use a comma when specifying multiple loan groups. |
<LOAN_PORTFOLIO_NO>
| Attribute | Comments |
|---|---|
| Value | The loan portfolio number. Use a comma when specifying multiple loan portfolios. |
<BORROWER_STATE>
| Attribute | Comments |
|---|---|
| Value | The state of the borrower’s address. Use a comma when specifying multiple states. |
<BRANCH_STATE>
| Attribute | Comments |
|---|---|
| Value | The state of the branch address. Use a comma when specifying multiple states. |
<ORIG_LOAN_AMOUNT_MAX>
| Attribute | Comments |
|---|---|
| Value | The maximum value of the original loan amount. |
<RATE>
| Attribute | Comments |
|---|---|
| Tn | The rate to use for each defined n term. |
Example
<RATELOOKUP>
<LOAN_GROUP_NO value="1,2">
<BORROWER_STATE value="CA,AZ,TX">
<ORIG_LOAN_AMOUNT_MAX value="5000">
<RATE T1="0.09836" T2="0.14673" T3="0.19458" T4="0.2419" T5="0.28871" T6="0.335" T7="0.3808" T8="0.4261" T9="0.4709" T10="0.51523" T11="0.55907" T12="0.60244" T13="0.64534" T14="0.68778" T15="0.72977" T16="0.7713" T17="0.81239" T18="0.85304" T19="0.89325" T20="0.93304" T21="0.9724" T22="1.01135" T23="1.04988" T24="1.088" T25="1.12572" T26="1.16304" T27="1.19996" T28="1.2365" T29="1.27265" T30="1.30842"/>
</ORIG_LOAN_AMOUNT_MAX>
<ORIG_LOAN_AMOUNT_MAX value="10000">
<RATE T1="0.09803" T2="0.14609" T3="0.19352" T4="0.24033" T5="0.28654" T6="0.33214" T7="0.37714" T8="0.42157" T9="0.46542" T10="0.5087" T11="0.55143" T12="0.5936" T13="0.63524" T14="0.67633" T15="0.71691" T16="0.75696" T17="0.7965" T18="0.83554" T19="0.87408" T20="0.91214" T21="0.94971" T22="0.9868" T23="1.02343" T24="1.05959" T25="1.0953" T26="1.13057" T27="1.16538" T28="1.19977" T29="1.23372" T30="1.26725"/>
</ORIG_LOAN_AMOUNT_MAX>
</BORROWER_STATE>
<BORROWER_STATE value="NY">
<RATE T1="0.09819" T2="0.14641" T3="0.19405" T4="0.24111" T5="0.28762" T6="0.33356" T7="0.37896" T8="0.42382" T9="0.46815" T10="0.51195" T11="0.55523" T12="0.59799" T13="0.64026" T14="0.68202" T15="0.72329" T16="0.76408" T17="0.80438" T18="0.84422" T19="0.88359" T20="0.92249" T21="0.96095" T22="0.99895" T23="1.03652" T24="1.07365" T25="1.11034" T26="1.14662" T27="1.18247" T28="1.21791" T29="1.25294" T30="1.28757"/>
</BORROWER_STATE>
</LOAN_GROUP_NO>
<RATE T1="0.09803" T2="0.14609" T3="0.19352" T4="0.24033" T5="0.28654" T6="0.33214" T7="0.37714" T8="0.42157" T9="0.46542" T10="0.5087" T11="0.55143" T12="0.5936" T13="0.63524" T14="0.67633" T15="0.71691" T16="0.75696" T17="0.7965" T18="0.83554"/>
</RATELOOKUP>